- LE FRAZIONI
- Che cosa sono
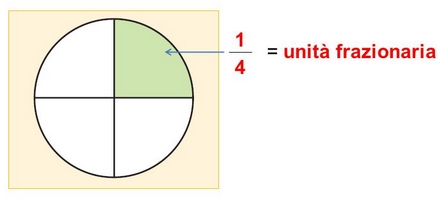
- La frazione indica il numero di parti in cui è stato diviso un intero (nell'esempio qui sotto sono QUATTRO) e il numero di parti che si prendono in considerazione (nell'esempio qui sotto UNA PARTE, quella verde).
- Le frazioni nei problemi
- I problemi con le frazioni si basano sempre su TRE elementi:
| una frazione |
| ESEMPIO: Alberto mangia i 5/7 di una torta che pesa 420 grammi. Quanti grammi di torta ha mangiato? |
| una quantità totale |
| ESEMPIO: Alberto mangia i 5/7 di una torta che pesa 420 grammi. Quanti grammi di torta ha mangiato? |
| una parte della quantità totale |
| ESEMPIO: Alberto mangia i 5/7 di una torta che pesa 420 grammi. Quanti grammi di torta ha mangiato? |
- 1° caso facile
- Ho la FRAZIONE, ho la QUANTITÀ TOTALE e...
| ...devo calcolare UNA PARTE DELLA QUANTITÀ TOTALE |
| ESEMPIO: Alberto mangia i 5/7 di una torta che pesa 420 grammi. Quanti grammi di torta ha mangiato? |
| quindi devo calcolare i 5/7 di 420 ->
trucchetto: divido sotto e moltiplico sopra -> 420 : 7 = 60 60 x 5 = 300 grammi |
| RISULTATO: Alberto ha mangiato 300 grammi di torta. |
- 1° caso difficile (con somma)
- Ho la FRAZIONE, ho la QUANTITÀ TOTALE e...
| ...devo calcolare PIU' PARTI DELLA QUANTITÀ TOTALE |
| ESEMPIO: La somma di due segmenti misura 190 cm e il minore è 1/4 del maggiore. Quanto misurano i DUE segmenti? |
| quindi devo calcolare DUE parti diverse della quantità totale ->
trucchetto: se il problema mi indica la SOMMA devo sommare i numeri della frazione -> 1/4 -> 1+4 = 5 e poi dividere il totale per quel numero -> 190 : 5 = 38 -> il numero così trovato sarà UNA PARTE DELLA QUANTITÀ TOTALE e basterà quindi moltiplicarla per le parti indicate dalla frazione per risolvere il problema 38 x 1 = 38cm segmento corto ----- 38 x 4 = 152cm segmento lungo |
- 1° caso difficile (con differenza)
- Ho la FRAZIONE, ho la QUANTITÀ TOTALE e...
| ...devo calcolare PIU' PARTI DELLA QUANTITÀ TOTALE |
| ESEMPIO: La differenza di due segmenti misura 42 cm e il minore è 2/9 del maggiore. Quanto misurano i DUE segmenti? |
| quindi devo calcolare DUE parti diverse della quantità totale ->
trucchetto: se il problema mi indica la DIFFERENZA devo sottrarre i numeri della frazione -> 2/9 -> 9-2 = 7 e poi dividere il totale(=qui è la differenza) per quel numero -> 42 : 7 = 6 -> il numero così trovato sarà UNA PARTE DELLA QUANTITÀ TOTALE e basterà quindi moltiplicarla per le parti indicate dalla frazione per risolvere il problema 6 x 2 = 12cm segmento corto ----- 6 x 9 = 54cm segmento lungo |
- 2° caso
- Ho la FRAZIONE, ho la PARTE DELLA QUANTITÀ TOTALE e...
| ...devo calcolare la QUANTITÀ TOTALE |
| ESEMPIO: Una botte contiene 32 litri, cioè i 4/9 della sua capacità. Quanti litri mancano per riempire la botte? |
| questi sono i problemi più difficili perchè la frazione si riferisce alla quantità totale, che noi NON conosciamo
ma basta ricordarsi questo trucco per risolverli: divido sopra e moltiplico sotto -> 32 : 4 = 8 8 x 9 = 72 litri = capacità totale della botte problema finito? NO! perchè il problema non chiedeva la capacità totale ma chiedeva quanti litri mancano per riempire la botte, quindi serve ancora un calcolo, una sottrazione -> 72 - 32 = 40 litri |
| RISULTATO: Per riempire la botte mancano 40 litri. |
- 3° caso
- Ho la QUANTITÀ TOTALE, ho la PARTE DELLA QUANTITÀ TOTALE e...
| ...devo calcolare la FRAZIONE |
| ESEMPIO: Alberto ha letto 40 pagine di un libro di 240 pagine. Qual è la frazione che esprime il numero di pagine lette da Alberto? |
| questi sono i problemi più facili perchè la frazione che ci viene chiesta... ce l'abbiamo già! basta ricordarsi questo trucco per risolverli:
numero più piccolo sopra e numero più grande sotto -> 40/240 e poi di solito semplificare -> 40/240 = 1/6 |
| RISULTATO: la frazione che esprime il numero di pagine lette da Alberto è un sesto. |
- Link utili
- Oltre 1000 PROBLEMI sulle frazioni, con difficoltà crescente e sistema di auto-correzione automatico
- L'elenco di tutti i nostri TUTORIAL
- Una raccolta delle migliori mappe concettuali sulle frazioni: MAPPA 01, MAPPA 02, MAPPA 03, MAPPA 04, MAPPA 05, MAPPA 06.
