- IL TRAPEZIO
- Che cos'è
- Si chiama trapezio ogni quadrilatero con due soli lati opposti paralleli chiamati BASI (nel disegno qui sotto B=base maggiore b=base minore). I lati non paralleli L1 e L2 si dicono LATI OBLIQUI. La distanza fra le due basi si chiama ALTEZZA. Ogni trapezio ha due DIAGONALI, una maggiore(nel disegno è quella verde) ed una minore. Il segmento evidenziato in rosso è una delle due PROIEZIONI dei lati obliqui sulla base maggiore.
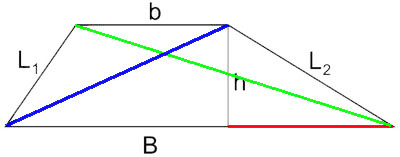
- Formule trapezio per problemi semplici
| PERIMETRO = | B+b+L1+L2 |
| AREA = | [(B+b)x h] : 2 |
| ALTEZZA = | 2 volte area : (B+b) |
| SOMMA DELLE BASI = | 2 volte area : h |
| BASE MAGGIORE = | (2 volte area : h) - b |
| BASE MINORE = | (2 volte area : h) - B |
- Il trapezio isoscele
- E' un tipo di trapezio con i LATI OBLIQUI UGUALI. Ha anche le DIAGONALI uguali e gli ANGOLI ADIACENTI alla relativa base uguali
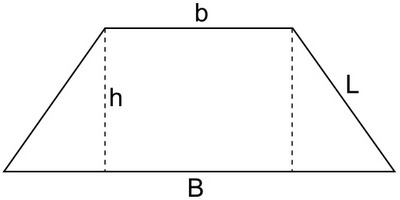
- Formule per problemi trapezio isoscele
| LATO OBLIQUO = | si usa il teorema di Pitagora radice quadrata di h² + (B-b/2)² |
| ALTEZZA = | si usa il teorema di Pitagora radice quadrata di L² - (B-b/2)² |
| PROIEZIONE LATO OBLIQUO = | si usa il teorema di Pitagora radice quadrata di L² - h² |
- Il trapezio rettangolo
- E' un tipo di trapezio con UN SOLO LATO OBLIQUO. L'altro lato obliquo è perpendicolare alle basi e forma quindi con loro due angoli retti. La diagonale maggiore (=D) forma un triangolo rettangolo.
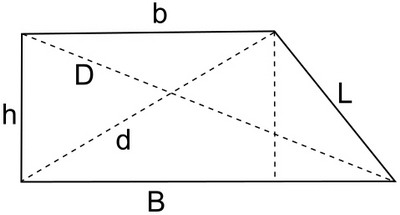
- Formule per problemi trapezio rettangolo
| LATO OBLIQUO = | si usa il teorema di Pitagora radice quadrata di h² + (B-b)² |
| ALTEZZA = (avendo lato obliquo e basi) |
si usa il teorema di Pitagora radice quadrata di L² - (B-b)² |
| ALTEZZA = (avendo una diagonale e una base) |
si usa il teorema di Pitagora radice quadrata di D² - B² |
| PROIEZ. LATO OBLIQUO = | si usa il teorema di Pitagora radice quadrata di L² - h² |
| DIAGONALE = | si usa il teorema di Pitagora radice quadrata di h² + B² (oppure b²) |
| BASE = | si usa il teorema di Pitagora radice quadrata di d² - h² |
- Link utili
- Oltre 200 PROBLEMI sul trapezio, con difficoltà crescente e sistema di auto-correzione automatico
- L'elenco di tutti i nostri TUTORIAL
- Una raccolta delle migliori mappe concettuali sul trapezio: MAPPA 01, MAPPA 02, MAPPA 03, MAPPA 04, MAPPA 05.
